3.4 Procesamiento computacional de SignoEscritura
Como se mencionaba anteriormente, los seres humanos a menudo trabajamos con conceptos e hipótesis que, tras un examen minucioso, no se encuentran definidos de manera exhaustiva ni formal. Esto resulta especialmente evidente al abordar el trabajo con imágenes. Si se inquiere a un especialista en radiología sobre la probabilidad de que una masa en la radiografía sea un tumor, o a un paleontólogo sobre por qué un determinado diente pertenece a un tiburón y no a un ratón, será complicado obtener una descripción matemática precisa, como la que requieren las máquinas. Los expertos pueden ofrecer una multiplicidad de razones y argumentos, pero la formalización mediante una lógica susceptible de ser computarizada resulta un desafío extremo, en ocasiones casi imposible. Las excepciones y el “sentido común” se acumulan, y conceptos aparentemente sencillos como “circular”, “proporción” o “textura” no se prestan fácilmente a una definición matemática inmediata.
En el ámbito de la imagen, uno de los obstáculos principales radica en su representación digital. Como en una cámara, o en la retina humana, podemos entender el medio visual como un campo plano y bidimensional de luz. Aunque biológica y neuronalmente nuestra visión es más compleja, esta es una aproximación suficiente en la que se fundamentan pantallas, impresoras y los formatos de imagen convencionales en el ordenador. La versión discreta de este campo físico de intensidades luminosas es una matriz bidimensional de puntos (píxeles), a los que asignamos una serie de valores para representar la luz correspondiente a esa posición en la imagen. No vamos a entrar aquí en teoría del color, pero debido a cómo lo percibimos los humanos, con tres tipos de células receptoras que responden a distintas longitudes de onda, la manera más habitual de representar la luz en una imagen es con tres intensidades: “rojo”, “verde” y “azul”, para cada uno de los píxeles (RGB).
Esta representación ilustra la brecha significativa que hay entre la imagen y la visión. Si los datos que poseemos son matrices bidimensionales de números, definir en base a esta representación lo que constituye un círculo, una línea, un polígono, más aún un diente, una letra o, en nuestro caso, un grafema de la SignoEscritura, no resulta trivial. Incluso el caso más sencillo, un segmento de recta, se torna en algo de complejidad asombrosa. Determinar qué píxeles corresponden a otros píxeles, dónde termina el segmento y comienza el fondo, cuál es el ángulo, en qué posición de la imagen se encuentra, todo ello requeriría ser codificado manualmente con reglas y una gran cantidad de excepciones. Además, dada la naturaleza imperfecta de la realidad, habría que incorporar modelos probabilísticos de cálculo complejo y definición desafiante.
Esta problemática forma parte de los desafíos de la inteligencia artificial clásica, pero, afortunadamente, es precisamente una de las cuestiones que resuelve la revolución del aprendizaje automático y, en particular, su versión más avanzada: el aprendizaje profundo o deep learning.
Este paradigma de la IA se fundamenta en inferir el modelo computacional directamente desde los datos, extrayendo patrones heurísticos e “intuiciones” que son difíciles de explicar, mediante el examen repetido de datos adecuadamente preparados. La preparación de datos o anotación, en nuestro caso descrita como parte del primer esfuerzo de ciencia de datos, es esencial, permitiendo que los algoritmos descubran las realidades subyacientes a los datos y las interpretaciones que se buscan.
El aprendizaje automático se fundamenta, desde una perspectiva algorítmica, en un principio esencial: la minimización del error. Este enfoque se basa en la disposición de una serie de datos y una predicción preliminar, corrigiéndose progresivamente el método de inferencia en función del error medido en las predicciones efectuadas. En muchos casos, se permite al algoritmo explorar de manera aleatoria durante un período determinado, e incluso avanzar en una “dirección incorrecta”, de modo que se puedan explorar distintas vías y soluciones hasta alcanzar una óptima. Esta solución óptima no suele ser única, y de hecho, estos algoritmos frecuentemente no son deterministas, llegando a una conclusión diferente cada vez que se ejecutan. La tarea del ingeniero consiste en manipular los distintos parámetros del algoritmo, las condiciones de contexto, y en ocasiones los propios datos y su pre-procesamiento, para lograr que el algoritmo encuentre con suficiente fiabilidad una solución óptima en términos de error de predicción.
La solución identificada se convierte en sí en un modelo del problema, una función que, al recibir datos conocidos o nuevos, ofrece una predicción sobre dichos datos. Esta predicción puede constituir información sobre el futuro, como el siguiente evento en una serie temporal o la previsión meteorológica para el día siguiente. También puede tratarse de información de “alto nivel”, que no está explícita en los datos brutos, como determinar si la matriz de píxeles se corresponde a un diente de tiburón, murciélago o si representa un perro. La predicción puede incluso consistir en reconstruir parte de la información original, que ha sido ocultada por los ingenieros a la red. En este modelo de aprendizaje “no supervisado”, no es necesario definir una tarea o etiquetar los datos, y se basa en entrenar a la red para que reconstruya diferentes partes de la entrada. Con suficientes datos de entrenamiento, este procedimiento permite al algoritmo aprender de forma íntima la estructura y apariencia de los datos, y es el procedimiento en el que se basan redes de última generación como las que crean los Deep Fakes o generan texto en lenguaje natural, como GPT.
La clave para todos estos avances, el Deep Learning, reside precisamente en lo que sugiere su nombre: aprendizaje profundo. Pero esta profundidad no es metafórica o conceptual, sino literal: las redes neuronales utilizadas en el Deep Learning constan de múltiples capas de procesamiento, donde cada capa recibe como entrada la salida de las capas anteriores. Esto les permite organizarse en niveles de abstracción: la primera capa simplemente detecta grupos de píxeles del mismo color, por ejemplo; la siguiente capa detecta segmentos de líneas rectas o arcos de curva; la capa subsiguiente compone estos pequeños patrones en formas más grandes, y así sucesivamente hasta llegar a una capa de clasificación o salida, que decide si la imagen es un perro o una bicicleta. Este funcionamiento es análogo a cómo opera el córtex visual humano; sin embargo, de la misma manera que no comprendemos en detalle cómo funciona este último, tampoco podemos afirmar con certeza qué hace cada capa o neurona de una red, limitándonos a observar patrones generales de funcionamiento. A pesar de que todo pueda parecer muy impreciso y poco determinista, y sea difícil creer incluso que pueda funcionar, el éxito de estos algoritmos es evidente y palpable incluso en nuestro entorno cotidiano.
3.4.1 El algoritmo YOLO de detección
Para la tarea concreta de reconocimiento de SignoEscritura, necesitamos algoritmos específicos en el dominio de la Visión Artificial. El primer algoritmo requerido es conocido como “You Only Look Once” (YOLO, Redmon et al. 2016). Este algoritmo es capaz de localizar los diferentes elementos constituyentes en una imagen (una tarea identificada como “detección”), además de asignarles una etiqueta (“clasificación”) dentro de las categorías previamente entrenadas. A tal fin, fracciona la imagen en pequeñas áreas y, para cada una, calcula la probabilidad de que dicha área represente un borde, esquina o zona interior de un objeto de interés, identificando también la clase del objeto. Posteriormente, estas probabilidades son ensambladas en regiones cuadrangulares, conocidas como “bounding boxes” (cajas delimitadoras), que constituyen el resultado del algoritmo: una lista de áreas en la imagen donde se encuentran los objetos identificados, junto con su etiqueta correspondiente.
Este algoritmo, en principio, resultaría adecuado para resolver la tarea propuesta: permite detectar los diferentes grafemas que forman un logograma, identificando cada uno de ellos y, en consecuencia, discerniendo su significado. Así comenzaron los estudiantes del trabajo de fin de grado aludido (Sánchez Jiménez, López Prieto, y Garrido Montoya 2019), pero pronto enfrentaron la dificultad de no contar con suficientes datos. Una debilidad inherente de los algoritmos de aprendizaje profundo radica en que, al operar de manera tan indiscriminada, requieren una considerable cantidad de datos para el aprendizaje efectivo. Si los datos y la capacidad de cómputo son limitados, no será viable alcanzar una solución con un error lo suficientemente reducido para ser útil. Por el contrario, incrementar la capacidad de cómputo sin aumentar los datos conduce al “overfitting” (sobreajuste), donde el algoritmo aprende a resolver exactamente la tarea con los datos presentados, sin ser capaz de generalizar a nuevos datos.
Además, es fundamental que los datos abarquen una proporción significativa, cuanto mayor mejor, del dominio de estudio, ya que las redes neurales tienen problemas para trabajar con datos fuera del dominio aprendido: interpolan mejor que extrapolan. Para que la red sea capaz de distinguir características comunes como rasgos independientes, estos deben manifestarse con suficiente frecuencia en los datos de entrenamiento. Por ejemplo, si solo existe una muestra de una mano en configuración “X” y con la palma hacia abajo, la red no distinguirá dos rasgos separados, configuración “X” y “palma hacia abajo”, sino que los interpretará como características indivisibles.
La gran cantidad de rasgos simultáneos existentes la fonología signada, reproducidos en la SignoEscritura, implica que este fenómeno ocurra con frecuencia en nuestro corpus de datos. Si se aplica una aproximación naïve, utilizando una única clase para cada grafema completamente distinto, se encontrarán combinaciones que solo aparecen una vez en el corpus, o incluso ninguna, obstaculizando el aprendizaje adecuado del algoritmo. Matemáticamente, podríamos decir, nos enfrentamos a un espacio altamente dimensional, con una (hiper) superficie por identificar pero de la que conocemos un conjunto de puntos notablemente poco denso.
3.4.2 Procesamiento aumentado con conocimiento experto
Para abordar este problema, es necesario desrarificar (hacer más denso) el espacio de búsqueda del problema, y para ello podemos utilizar las múltiples etiquetas codificadas en el corpus a las que hemos hecho referencia en la sección previa. En un procedimiento reconocido comúnmente en ingeniería como “divide y vencerás”, separamos el proceso de reconocimiento en varias etapas consecutivas, cada una de ellas más sencilla de resolver que la tarea en su totalidad.
En primer lugar, solicitamos al detector (YOLO) que identifique los grafemas, aunque no se requiere que los clasifique completamente, sino únicamente que determine la clase de grano grueso. Esto implica que el algoritmo puede generalizar y aprender que, por ejemplo, los grafemas para la cabeza suelen tener un tamaño similar y más grande que los de las manos, etc. Una vez identificados los grafemas, podemos utilizar una red especializada en clasificación, en nuestro caso “Alexnet” (Krizhevsky, Sutskever, y Hinton 2017), que no necesita aprender a localizar los diferentes grafemas dentro del logograma. De hecho, es posible utilizar distintas redes para las manos, las cabezas, etc., permitiendo que estas redes aprendan los detalles más finos de esas clases sin tener que distinguirlas de las demás.
Para las manos, no obstante, esta idea no es suficiente. Existen más de medio centenar de configuraciones posibles de la mano, representadas cada una por formas de grafema diferentes. Además, como hemos visto anteriormente, cada una de ellas puede aparecer rotada o con distinto relleno de color, multiplicando de manera exponencial los grafemas a reconocer.
Por tanto, debemos codificar de alguna manera el conocimiento que tenemos sobre la rotación de los grafemas en nuestro algoritmo. Es fundamental aclarar que esto es algo que las redes pueden aprender por sí mismas, pero requiere una mayor cantidad de datos de la que disponemos. Experimentos preliminares para aumentar artificialmente la cantidad de datos (“data augmentation”) no resultaron exitosos, por lo que se necesitó otra aproximación.
Afortunadamente, ni la rotación ni la simetría son procesos difusos, como la definición de una línea, un diente o un perro. Son, en cambio, procesos deterministas, matemáticamente bien definidos y que podemos calcular en el ordenador. Si utilizamos esta lógica de manera externa al algoritmo, éste no tiene por qué aprenderla, y se ve liberado para aprender otros detalles. Podemos ver esta técnica como una de densificación de datos o compresión de características, ya que al eliminar los grados de libertad que crean las rotaciones reducimos la dimensionalidad del espacio del problema.
En una primera aproximación, se intentó rotar los grafemas de mano detectados, generando todas las posibilidades posibles y clasificando cada una de ellas. La elección se basaría en la rotación que la red clasificase con mayor confianza, descartando las demás. No obstante, este enfoque resultó problemático debido a la elevada cantidad de falsos positivos, en los que la red seleccionaba la rotación incorrecta o varias de ellas con una alta confianza.
La solución encontrada finalmente consistió en dividir de nuevo el problema para conquistarlo. Tras detectar las manos en el logograma, se entrenó una red clasificadora con el propósito exclusivo de determinar la transformación (rotación y simetría) del grafema. Una vez identificada, esta transformación puede ser revertida fácilmente mediante un proceso determinista, de manera que se obtiene un grafema siempre en orientación “erguida”. Así, es posible entrenar redes clasificadoras para decidir las etiquetas subsiguientes (forma y variación) que no tienen que tener en cuenta la posible transformación geométrica del grafema.
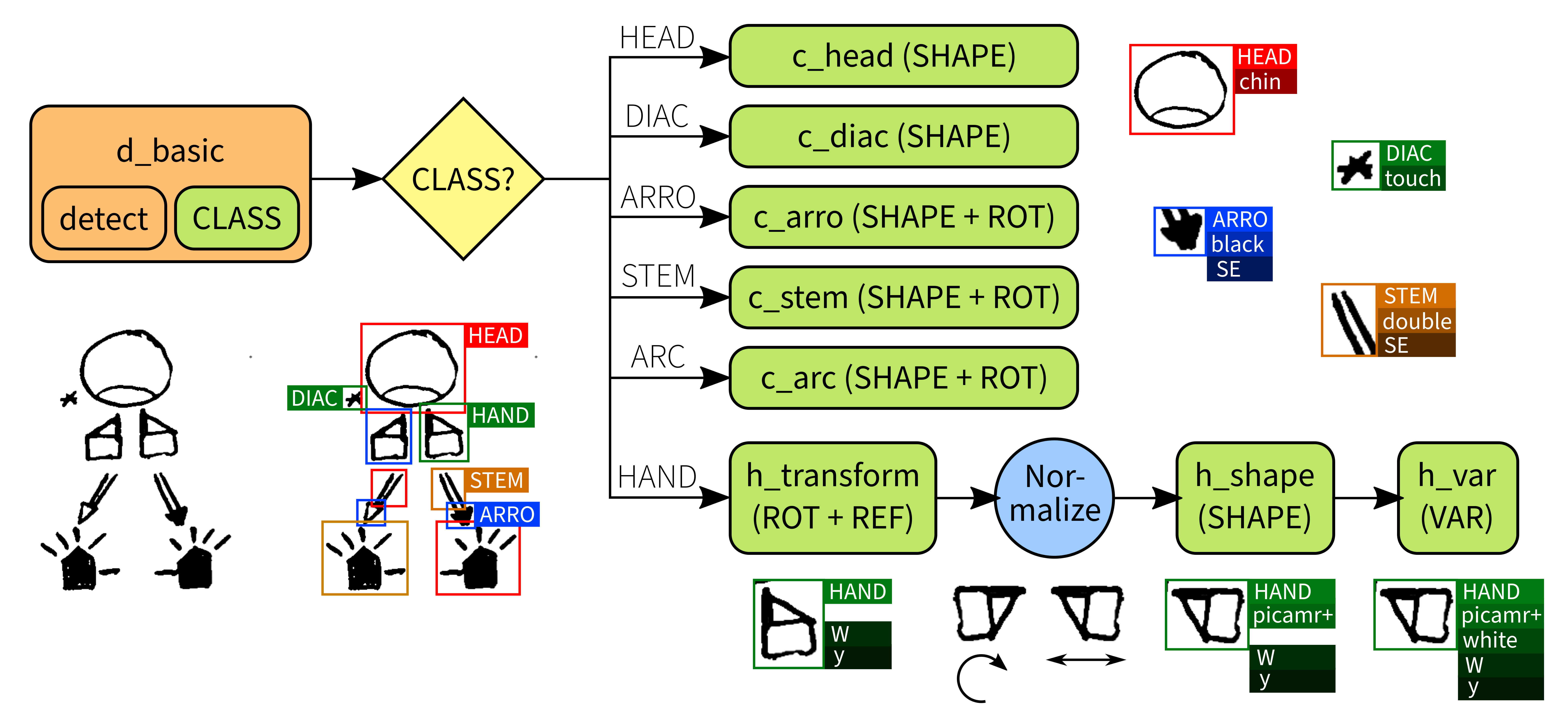
Todo el proceso fue programado en un “pipeline”, representado en la figura 3.6. Este “pipeline” de decisiones, el entrenamiento de las diversas redes neuronales y, en general, todo el desarrollo programático, forman parte nuevamente de Quevedo, que se describe con mayor detalle en la sección 3.5.1 y en los capítulos 9 y 10.
Para evaluar los resultados de nuestra algoritmia, recurrimos al “acierto” (accuracy), una métrica de evaluación equilibrada y que tiene la ventaja añadida de permitir una comparación directa entre nuestra solución y el enfoque base directo. Se formula como la proporción directa de predicciones correctas en el total de predicciones realizadas y potenciales. El aspecto clave a evaluar son los grafemas pronosticados: cuántos de ellos pueden ser encontrados y qué tan precisas son sus características pronosticadas. Medimos este acierto con tres cálculos: el acierto en la detección de los grafemas, el acierto en su clasificación (es decir, la predicción de sus etiquetas) y una medida combinada que puntúa cada solución para la tarea integral de reconocer la SignoEscritura.
Tras evaluar el acierto de los distintos algoritmos, concluimos que nuestra aproximación experta, basada en el pipeline adaptativo, mejora el algoritmo YOLO directo en un 17%, alcanzando un acierto global del 68%. En concreto, este enfoque mejora sustancialmente la detección de grafemas. Al detectar mayor número de ellos, incrementa la detección de instancias que son “difíciles de predecir”, lo cual provoca una leve disminución en el acierto de clasificación. No obstante, globalmente se observa la mejora cuantitativa del 17% antes mencionada. Adicionalmente, desde un análisis cualitativo, las nuevas predicciones resultan mucho más aplicables. Detectar la mayoría de los grafemas presentes, incluso si algunas de sus etiquetas son incorrectas, incrementa significativamente la utilidad y aplicabilidad práctica de los resultados.
El objetivo principal de nuestro desarrollo no consistía en la evaluación de las capacidades inherentes a las redes neuronales o los algoritmos individuales, sino en explorar la viabilidad de aplicar nuestro conocimiento experto, adquirido a través del análisis teórico, para facilitar un procesamiento más eficiente en un dominios como la SignoEscritura o la LS, caracterizados por la escasez de datos. Los resultados obtenidos, que muestran una mejora significativa en la tasa de acierto, corroboran la validez de nuestra enfoque metodológico. Este hallazgo sugiere que, incluso en ausencia de grandes volúmenes de datos —tan comunes en los enfoques computacionales contemporáneos—, la selección meticulosa de los datos y la aplicación de conocimientos teóricos específicos al dominio en cuestión pueden no sólo mejorar, sino incluso habilitar, el procesamiento computacional eficaz.
Para obtener información más detallada sobre la evaluación, incluida la formulación matemática y los datos numéricos, se puede consultar el capítulo 8, en el que se ofrece un análisis más detallado de la algoritmia empleada.